Arbori de intervale

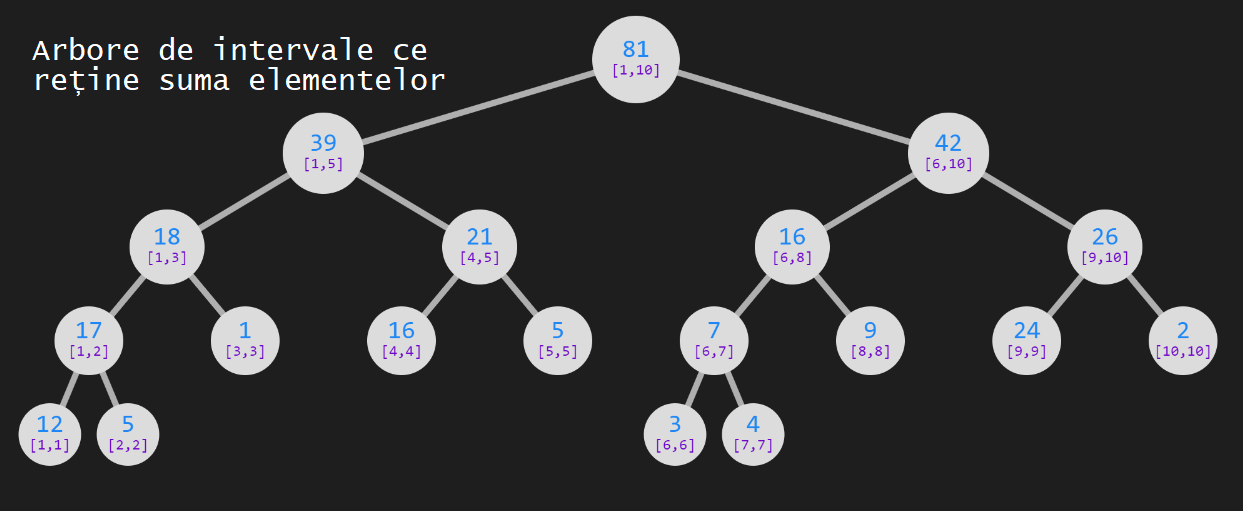
Un arbore de intervale este un arbore binar complet în care în fiecare nod reţinem răspunsul pentru un anumit interval. Considerăm vectorul tree de dimensiune $4 * N$, în care dorim să efectuăm operaţiile de $update$ şi $query$. Rădăcina va reţine răspunsul pentru intervalul $[1, n]$. Pentru fiecare nod reţinem răspunsul pentru intervalul $[st, dr]$, unde $st$ <= $dr$, iar fiul din stânga va reţine răspunsul pentru intervalul $[st, mij]$, pe când fiul din dreapta răspunsul pentru intervalul $[mij + 1, dr]$, unde $mij = (st + dr) / 2$.
Intervalul $[st, dr]$ asociat unui nod se numeşte interval standard. Frunzele arborelui sunt considerate intervale elementare, ele având lungimea $1$.

Un arbore de intervale este un arbore binar echilibrat (diferenţa absolută între adâncimea subarborelui stâng îi cea a subarborelui drept este cel mult $1$). Astfel, adâncimea unui arbore de intervale care conţine intervale incluse în $[1, N]$ este $[\log_2 n]$ + $1$, şi tocmai din acest motiv timpul de execuţie pentru operaţiile de update, respectiv query este de $O(\log_2 n)$.
Un arbore de intervale necesită memorie de $4 * N$.
Dacă valoarea nodului care reţine intervalul $[st, dr]$ este $node$, valoarea nodului care reţine fiul din stânga este $2 * node$, iar valoarea nodului care reţine fiul din dreapta este $2 * node + 1$.

Începem să căutăm din rădăcină poziţia elementului pe care trebuie să-l actualizăm. În funcţie de intervalul care conţine poziţia căutată ne deplasăm fie pe fiul din stânga, fie pe cel din dreapta. Odata ce am ajuns în frunză, actualizăm valoarea poziţiei şi utilizăm o abordare de tipul $bottom-up$ până la rădăcină, pentru a schimba şi valoarea intervalelor în care se află poziţia modificată.

Căutăm răspunsul la un query pe intervalul $[x, y]$, astfel: recursiv din rădăcină începem să verificăm dacă intervalul reprezentat de nodul actual se află complet în intervalul căutat. Dacă da, returnăm valoarea nodului.

Folosim lazy update în momentul în care trebuie să modificăm valoarea din fiecare poziţie din intervalul $[st, dr]$, pentru a nu risca ca un update care în mod normal se face în $O(\log_2 n)$, să-l facem în $O(n\log_2 n)$. Astfel vom mai folosi un vector, $lazy$, în care vom reţine că trebuie sa modificăm valorile din intervalul $[st, dr]$, iar când vom avea nevoie de valoarea unei poziţii din intervalul $[st, dr]$, vom propaga $lazy-ul$ la cei $2$ fii până ajungem la poziţia căutată.