Intersecție segmente
Se dau $n$ segmente în plan, prin coordonatele extremităților acestora ($x_1, y_1, x_2, y_2$). Știind că fiecare segment este paralel cu una dintre axele de coordonate, să se determine numărul de intersecții formate de segmentele date.
Restricții
- $1 \le n \le 100.000$
- $1 \le x_1, y_1, x_2, y_2, \le 300.000$
- Oricare două puncte date sunt distincte.
Exemplu
| Input | Output | Explicație |
|---|---|---|
5
|
3
|
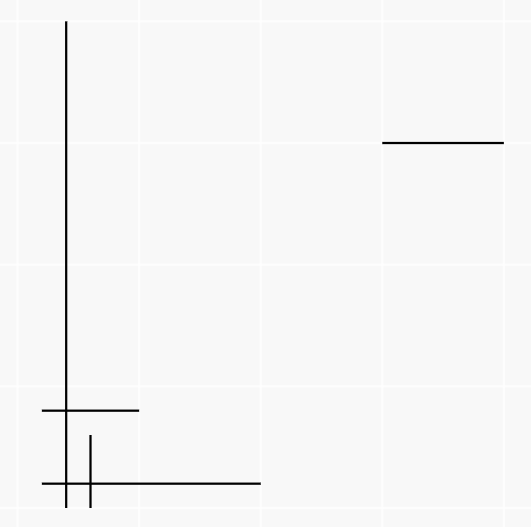
|
Soluție
Soluția naivă constă în a alege fiecare două segmente și a testa dacă acestea se intersectează. Complexitatea este $O(n^2)$. Din nou, prea ineficient.
Aceasta e o problemă clasică de baleiere. Vom construi un vector cu 3 tipuri de evenimente:
- începutul unui segment orizontal
- sfârșitul unui segment orizontal
- apariția unui segment vertical
Sortăm acest vector crescător după abscise, iar apoi facem o baleiere pe el astfel: Când întâlnim un început de segment orizontal, de ordonată $y$, facem $\mathrm{update}(y, +1)$.
Când întâlnim un segment vertical, cu extremitățile de ordonate $y_1$ și $y_2$ ($y_1 \lt y_2$), adăugăm la soluție $\mathrm{query}(y_1, y_2)$. Acest apel va returna numărul de segmente orizontale active (care încă nu s-au închis) ce au $y$-ul cuprins între $y_1$ și $y_2$, deci care automat intersectează segmentul vertical curent.
Când întâlnim sfârșitul unui segment orizontal, de ordonată $y$, facem $\mathrm{update}(y, -1)$, scoțând segmentul din arborele de intervale.
Cum sortarea se face în $O(n \log_2 n)$, iar baleierea împreună cu operațiile pe arborele de intervale se fac tot în $O(n \log_2 n)$, complexitatea acestei soluții este $O(n \log_2 n)$.
Notă: În această problemă, $\mathrm{update}(x, y)$ înseamnă că la poziția $x$ se adaugă valoarea $y$, nu se înlocuiește cu $y$.
int main() { int n; cin >> n; vector<Event> ev; for (int i = 0; i < n; i++) { int x1, y1; fin >> x1 >> y1; int x2, y2; fin >> x2 >> y2; if (y1 == y2) { ev.push_back(Event(+1, min(x1, x2), y1)); // începutul unui segment orizontal ev.push_back(Event(-1, max(x1, x2), y1)); // sfârșitul unui segment orizontal } else ev.push_back(Event(0, x1, min(y1, y2), max(y1, y2))); // segment vertical } SegmTree tree(300000); sort(ev.begin(), ev.end()); int sol = 0; for (Event it : ev) if (it.type) tree.update(it.y1, it.type); else sol += tree.query(it.y1, it.y2); cout << sol << '\n'; return 0; }