|
||||||||||||||||||||||||
|
ultima problemă
grupă: mică
sursă: OMI 2016 ultimul articol
autor: Prof. Radu Vişinescu
ultimul software
autor: Prof. Emanuela Cerchez
|
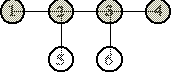
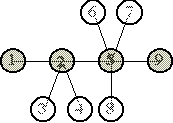
Definitie: O "omida" este un arbore cu urmatoarea proprietate: exista un lant central astfel încât fiecare nod al arborelui fie apartine lantului central fie este adiacent lantului. Figurile de mai jos ilustreaza doua "omizi", nodurile gri indicând lantul.
Pot exista mai multe lanturi. De exemplu, un alt lant pentru "omida" 2 este 3-2-5-9. Cerinte Scrieti un program care, fiind data o "omida" cu N noduri, va eticheta nodurile cu numere de la 1 la N ce satisfac conditiile:
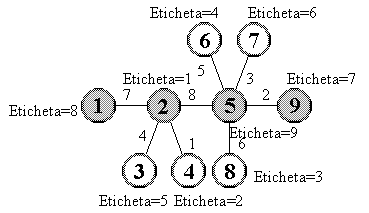
Mai jos este ilustrat un mod de etichetare a "omidei" 2. Modulele diferentelor sunt indicate pe muchiile respective.
Date de intrare Fisierul de intrare omida.in
contine pe prima linie N, un numar întreg ce indica numarul
de noduri. Fiecare dintre urmatoarele N-1 linii contine X Y doua numere întregi,
separate printr-un spatiu, reprezentând doua noduri adiacente conectate
cu o muchie. Date de iesire Fisierul de iesire omida.out contine o singura linie care contine L1 L2 ... LN (N numere întregi, separate prin cate un spatiu, unde Li reprezinta eticheta asociata nodului i). În cazul când exista mai multe solutii, se va prezenta numai una. Daca nu este posibila nici o etichetare, fisierul de iesire va contine pe unica linie cuvântul IMPOSIBIL. Restrictii
Exemplu Fisierul de intrare omida.in descrie "omida" din Figura 2, iar fisierul de iesire omida.out descrie etichetarea din Figura 3.
propunător: Prof. Emanuela Cerchez emanuela.cerchez@gmail.com Articole recomandate
Probleme recomandate
|
|||||||||||||||||||||||
| surse trimise | ajutor |