Andrei este un maestru al jocului de tetris, îl poate juca zile întregi cu ochii închişi şi cu mâinile legate la spate. De aceea el a hotărât să treaca la un alt nivel şi să joace varianta 3D a jocului.
Piesele vor cădea pe o suprafaţă plană orizontală de formă pătrată, cu latura de M cm, denumită baza. Pe bază este trasat un caroiaj ce delimitează MxM pătrăţele de latură 1 cm, fiecare pătrăţel fiind identificat prin coordonatele sale (linia şi coloana pe care se află).
După căderea unor piese pe bază, se obţine o anumită configuraţie de joc, ce va fi reprezentată ca o matrice B cu M linii şi M coloane, Bij fiind înălţimea atinsă de cel mai înalt cub plasat pe pătrăţelul de pe linia i şi coloana j al matricei (1≤i,j≤M) - vezi figura 1.
O piesă a jocului se obţine prin lipirea unor cuburi de latură 1 cm pe o suprafaţă plană (baza piesei) - vezi figura 2. O piesă va fi reprezentată de asemenea ca o matrice P cu N linii şi N coloane, Pij fiind numărul de cuburi aşezate pe pătratul de pe linia i şi coloana j al bazei piesei (1≤i,j≤N).
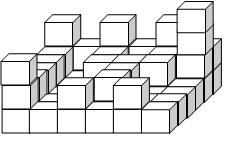
Configuraţia bazei din figura de mai sus va fi descrisă de următoarea matrice:
3 2 3 2 3 2
2 1 2 1 2 4
2 1 2 2 2 1
2 1 1 2 1 1
2 1 1 2 1 1
3 1 2 1 2 1
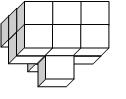
Piesa din figura precedenta va fi descrisă de următoarea matrice:
1 2 1
2 3 2
2 2 2
Fiecare pătrăţel al bazei piesei sau al bazei are cel puţin un cub aşezat pe el.
Piesele vor cădea cu baza piesei în sus şi nu pot fi rotite. O piesă se poziţionează pe bază astfel: se aliniază pătratul (1,1) al bazei piesei cu un pătrăţel (L,C) al matricei (fără ca piesa să depăşească limitele bazei), iar piesa cade vertical până când un cub al piesei atinge un cub al bazei.
Spunem că o piesă se poziţionează perfect într-o anumită poziţie (L,C) dacă pentru fiecare pătrăţel al bazei piesei cubul ″cel mai de jos″ atinge cubul situat la înălţime maximă de pe pătrăţelul bazei corespunzător.
Cerinţă
Date fiind configuraţia bazei şi o piesă, să se determine numărul de poziţii în care piesa poate fi poziţionată perfect.
Date de intrare
Fişierul de intrare
tetris2.in conţine pe prima linie numărul natural M, reprezentând dimensiunea bazei. Următoarele M linii conţin câte M numere naturale separate prin spaţii, reprezentând matricea care codifică configuraţia bazei. Pe linia M+2 se află numărul natural N, reprezentând dimensiunea bazei piesei. Pe următoarele N linii se află câte N numere naturale separate prin spaţii, reprezentând matricea ce codifică piesa.
Date de ieşire
Fişierul de ieşire
tetris2.out va conţine o singură linie pe care va fi scris numărul de poziţii în care piesa dată poate fi poziţionată perfect.
Restricţii
1 < M < 505
0 < N < 101
N < M
1 ≤ Mi,j ≤ 10000 (1≤i, j≤M)
1 ≤ Pi,j ≤ 10000 (1≤i, j≤N)
Exemple
tetris2.in | tetris2.out | Explicaţii |
6
3 2 3 2 3 2
2 1 2 1 2 4
2 1 2 2 2 1
2 1 1 2 1 1
2 1 1 2 1 1
3 1 2 1 2 1
3
1 2 1
2 3 2
2 2 2
| 1
| Piesa poate fi poziţionată perfect doar în poziţia (1,3). |

