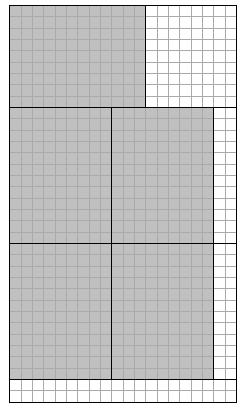
C.C, elev într-a 9-a, viseaza sa termine odata scoala si sa se angajeze la firma tatalui sau, firma de papetarie, publicitate si reclame luminoase. Pentru început i s-a promis postul de muncitor la departamentul "Cartoane" si aici îl asteapta cartoane dreptunghiulare de diferite dimensiuni din care trebuie sa obtina alte cartoane dreptunghiulare, mai mici, prin taierea cartoanelor mari cu ajutorul unui dispozitiv mecanic numit ghilotina.
Pentru a fi promovat în functia de sef al departamentului "Cartoane", el are de rezolvat o problema de proiectare a procesului de taiere: pentru un carton dreptunghiular de dimensiuni L si H date, se cere sa se gaseasca o modalitate de taiere cu ajutorul ghilotinei pentru a obtine un numar maxim de cartonase dreptunghiulare de dimensiuni A si B date. Se stie ca tehnologia admisa presupune asezarea dreptunghiului initial în orice pozitie, taierea lui în fâsii dreptunghiulare orizontale de diverse latimi si apoi taierea fiecarei fâsii, prin taieturi paralele, în dreptunghiuri mai mici.

Cerinta

Pentru dimensiunile L si H ale cartonului initial si dimensiunile A si B ale cartonaselor comandate de client, sa se determine numarul maxim da cartonase care se pot obtine din cartonul initial prin aplicarea acestei tehnologii.

Date de intrare

Fisierul de intrare cartonase2.in contine pe prima linie numerele natural L H, separate printr-un spatiu, reprezentand dimensiunile cartonului initial. Pe cea de a doua linie se afla numere naturale A si B separate printr-un spatiu, care reprezinta dimensiunile fiecaruia dintre cartonasele comandate.

Date de iesire

Fisierul de iesire cartonase2.out va contine o singura linie pe care se scrie un singur numar reprezentând numarul maxim de cartonase care se pot obtine.

Restrictii si precizari

• 1 <= L, H <= 1000
• 1 <= A, B <= 50
• Toate datele de intrare sunt numere naturale.
  

Exemplu

prof. Rodica Pintea
Liceul "Grigore Moisil" Bucuresti
Contact:ro_dica@yahoo.com