| acop |
|
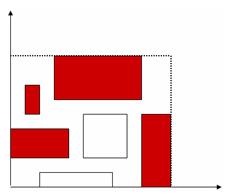
| Fie un chenar dreptunghic de lungime W unitati si latime H unitati, plasat cu coltul din stanga jos in originea sistemului de coordonate si avand laturile paralele cu axele. In acest chenar sunt desenate N dreptunghiuri, de asemenea cu laturile paralele cu axele. Se numeste acoperire a chenarului un set de dreptunghiuri selectate dintre cele N si asezate astfel incat, oricum am trasa o paralela la Ox sau o paralela la Oy prin chenar, aceasta sa intersecteze cel putin un dreptunghi (interiorul sau laturile) din acoperire. Cerinţă Sa se determine cardinalul minim al unei acoperiri a chenarului, precum si numarul de acoperiri de cardinal minim. Date de intrare Fisierul de intrare acop.in contine pe prima linie T, numarul de date de test din fisier. Urmeaza T blocuri unul dupa altul, fiecare bloc avand structura fixa. Pe prima linia a unui bloc sunt doua numere naturale W si H, reprezentand dimensiunile chenarului. A doua linie din fiecare bloc contine un numar natural N, reprezentand numarul de dreptunghiuri. Fiecare din urmatoarele N linii, pana la sfarsitul blocului, contine cate 4 numere (x1 y1 x2 y2), reprezentand doua colturi diametral opuse ale unui dreptungi. Toate numerele de pe aceeasi linie sunt superate de cate un spatiu. Date de ieşire Fisierul de iesire acop.out va contine T linii, pe fiecare fiind scris raspunsul pentru blocul corespunzator din fisierul de intrare. Fiecare linie va contine 2 numere naturale: cardinalul minim posibil pentru o acoperire si numarul de acoperiri optime, despartite de exact un spatiu. Daca nu exista nicio acoperire posibila, pe linia respectiva se va afisa doar -1. Restricţii
Exemplu
|