3d

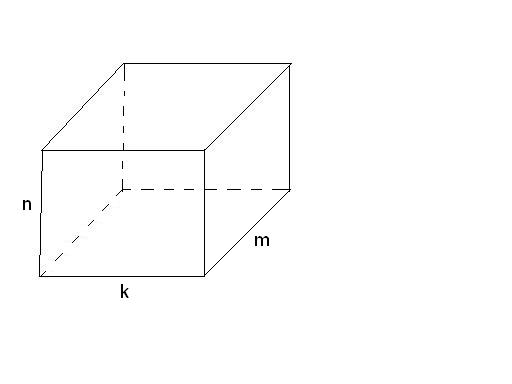
Se dă un tablou tridimensional cu m linii, k coloane şi înălţime n (vezi figura de mai jos), care poate conţine doar 0 şi 1.

Cerinţă

Să se determine subtabloul de volum maxim, care conţine doar 0 în interior. Un subtablou se poate defini prin coordonatele (x1,y1,z1) şi (x2,y2,z2) ale colţurilor, unde 1 <= x1 <= x2 <= n, 1 <= y1 <= y2 <= m, 1 <= z1 <= z2 <= k. Subtabloul conţine toate elementele cu coordonatele (x,y,z), unde x1 <= x <= x2, y1 <= y <= y2, z1 <= z <= z2.

Date de intrare

Pe prima linie a fişierului de intrare 3d.in se află numerele n, m şi k, separate printr-un singur spatiu. Pe următoarele n*m linii se află câte k numere separate prin câte un spaţiu, semnificând elementele tabloului.

Date de ieşire

În fişierul de ieşire 3d.out să se afişeze volumul maxim ce se poate obţine.

Restrictii

• 1 <= n, m, k <= 50

Exemplu