herbert
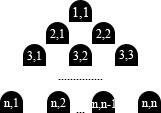
Micul robotel Herbert s-a saturat sa tot alerge dupa butonase albe in griduri dreptunghiulare asa ca s-a hotarat sa accepte un nou tip de sarcina. El a fost asezat intr-o zona "triunghiulara" de dimensiune n (zona este formata din n linii astfel: pe prima linie se afla o locatie, pe a doua linie se gasesc 2 locatii...etc pe linia n se gasesc n locatii), ca in figura:

Fiecare locatie din zona este identificata prin doua coordonate numere naturale (prima coordonata reprezinta linia, iar a doua diagonala la care se afla locatia respectiva). Atunci cand Herbert se afla la coordonatele (x,y) el se poate deplasa doar in una din cele 6 locatii vecine: (x-1,y-1), (x-1,y), (x,y+1), (x+1,y+1), (x+1,y), (x,y-1).
Sarcina robotelului este sa plece dintr-o locatie initiala (xs,ys) si sa ajunga la o locatie finala (xf,yf) trecand prin toate locatiile triunghiului o singura data (inclusiv prin cea initiala si cea finala va trece o singura data). Locatia initiala si cea finala nu coincid niciodata.
Insa Herbert e un robotel care se plictiseste repede. Asadar, pentru ca el sa nu poata fugi din zona triunghiulara, nu va avea niciodata locatiile de inceput si de sfarsit fixate pe laturi. O locatie (x,y) se afla pe laturi daca: y = 1 sau x = y sau x = n. Fiind si idealist, va refuza din start acele sarcini care i se par redundante. Nu va accepta ca numarul liniei pe care se afla locatia finala sa fie mai mica decat numarul liniei pe care se afla locatia initiala (adica xf < xs) pentru ca parcurgand drumul invers, intr-o astfel de configuratie, poate sa reduca problema la cazul xs < xf. Asadar xs va fi mereu strict mai mic decat xf.
Cerinta
Sa se determine pentru robotel un drum care trece prin toate locatiile triunghiului
exact o data. Drumul trebuie sa inceapa in (xs,ys)
si sa se termine in (xf,yf).
Date de intrare
Fisierul de intrare herbert.in are urmatoarea structura:
- pe prima linie este scris numarul
natural n reprezentand dimensiunea
zonei triunghiulare;
- pe cea de-a doua linie se gasesc 2
numere naturale separate printr-un spatiu, xs
ys, reprezentand coordonatele locatiei de start;
- pe cea de-a
treia linie se gasesc 2 numere
naturale separate printr-un spatiu, xf yf,
reprezentand coordonatele locatiei finale.
Date de iesire
Fisierul de iesire herbert.out
va contine n(n + 1)/2 linii care
descriu drumul gasit astfel:
- pe prima linie se scriu 2 numere
naturale separate printr-un spatiu reprezentand coordonatele locatiei din care
se pleaca xs ys
- pe cea de-a doua linie se scriu 2
numere naturale separate printr-un spatiu reprezentand coordonatale locatiei
ce urmeaza in drum dupa
(xs,ys)
...
- pe linia n(n+1)/2
se gasesc 2 numere naturale separate printr-un spatiu
reprezentand coordonatele locatiei finale (xf,yf)
Restrictii
Exemplu
5
herbert.in
herbert.out
3 2
4 23 2
3 1
2 1
1 1
2 2
3 3
4 4
5 5
5 4
4 3
5 3
5 2
5 1
4 1
4 2
Timp maxim de executie/test: 0.1 secunde
Iolanda Popa
studenta - Facultatea de Informatica, Iasi
Contact: iolivp@gmail.com