herbert
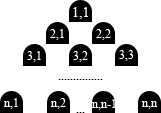
Little robot Herbert has had enough of running after white buttons in rectangular grids so it decided to accept a new kind of task. It was placed in a triangular area of size n (the area is comprised of n lines, as follows: on line one there is one location, on line two there are 2 locations...etc. on line n there are n locations), just like in this image:

Every location from the area is identified by two positive integer coordinates (the first represents the line and the second the diagonal of that location). When Herbert is at coordinates (x,y), it can move only in one of the 6 neighboring locations: (x-1.y-1), (x-1.y), (x,y+1), (x+1.y+1), (x+1.y), (x,y-1).
The task of the little robot is to go from an initial location (xs,ys) and get to a final location (xf,yf), going through all the locations of the triangle only once (it will also go through the initial and final locations only once). The initial and final locations are never the same.
But Herbert is a little robot that gets bored really fast. So, in order for it not to be able to escape from the triangular area, it will never have initial and final locations on the sides. A location (x,y) is located on the sides if: y = 1 or x = y or x = n. Herbert also being an idealist, it will refuse those tasks that seem redundant. It will never accept for the line number of the final location is on to be smaller than that of the line number of the initial location (namely xf < xs) because by going the route in the other direction, in such a configuration, it can reduce the program to the xs < xf case. Therefore, xs will always be smaller than xf.
Task
Determine a route for the little robot that goes through all the triangle's locations only once. The route must begin in (xs,ys) and end in (xf,yf).
Input Data
Input file herbert.in has the following structure:
- line one contains positive integer n representing the size of the triangular area;
- line two contains 2 positive integers separated by a space, xs ys, representing the coordinates of the initial location;
- line three contains 2 positive integers separated by a space, xf yf, representing the coordinates of the final location.
Output Data
Output file herbert.out will contain n(n + 1)/2 lines describing the found route as follows:
- on line one we will write 2 positive integers separated by a space representing the coordinates of the initial location, xs ys
- on the second line we will write 2 positive integers separated by a space representing the coordinates of the next location after
(xs,ys)
...
- on line n(n+1)/2 we will have 2 positive integers separated by a space representing the coordinates of the final location, (xf,yf)
Restrictions
Example
5
herbert.in
herbert.out
3 2
4 23 2
3 1
2 1
1 1
2 2
3 3
4 4
5 5
5 4
4 3
5 3
5 2
5 1
1 4
4 2
Time limit: 0.1 seconds/test
Iolanda Popa
student - IT College, Iaşi
Contact: iolivp@gmail.com