cartonase
C.C, elev
într-a 9-a, viseaza sa termine odata scoala si sa se angajeze la firma
tatalui sau, firma de papetarie, publicitate si reclame luminoase. Pentru început
i s-a promis postul de muncitor la departamentul "Cartoane" si aici
îl asteapta cartoane dreptunghiulare de diferite dimensiuni din care trebuie
sa obtina alte cartoane dreptunghiulare, mai mici, prin taierea cartoanelor
mari cu ajutorul unui dispozitiv mecanic numit ghilotina.
Pentru a fi promovat în functia de sef al departamentului "Cartoane",
el are de rezolvat o problema de proiectare a procesului de taiere: pentru un
carton dreptunghiular de dimensiuni L
si H date, se cere sa se gaseasca
o modalitate de taiere cu ajutorul ghilotinei pentru a obtine un numar maxim
de cartonase dreptunghiulare de dimensiuni A
si B date. Se stie ca tehnologia
admisa presupune asezarea dreptunghiului initial în orice pozitie, taierea
lui în fâsii dreptunghiulare orizontale de diverse latimi si apoi
taierea fiecarei fâsii, prin taieturi paralele, în dreptunghiuri
mai mici.
Cerinta
Pentru dimensiunile
L si H
ale cartonului initial si dimensiunile A
si B ale cartonaselor comandate
de client, sa se determine numarul maxim da cartonase care se pot obtine din
cartonul initial prin aplicarea acestei tehnologii.
Date de
intrare
Fisierul de intrare cartonase.in
contine pe prima linie numerele natural L
H, separate printr-un spatiu, reprezentand dimensiunile cartonului initial.
Pe cea de a doua linie se afla numere naturale A
si B separate printr-un spatiu,
care reprezinta dimensiunile fiecaruia dintre cartonasele comandate.
Date de
iesire
Fisierul de iesire cartonase.out
va contine o singura linie pe care se scrie un singur numar reprezentând
numarul maxim de cartonase care se pot obtine.
Restrictii
si precizari
- 1 <= L, H <= 1000
- 1 <= A, B <= 50
- Toate datele de intrare
sunt numere naturale.
Exemplu
|
cartonase.in |
cartonase.out
|
Explicatie |
35
20
9 12
|
5
|
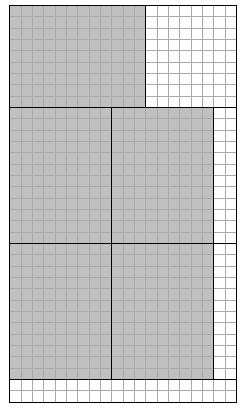
Se aseaza dreptunghiul
"pe înaltime", se taie 4 fâsii orizontale (o fâsie
de 9, doua de 12 si una de 2), prima fâsie se taie în doua
bucati (de 12, respectiv de 8), celelalte doua fâsii se taie fiecare
în 3 bucati (câte doua de 9 si una de 2). Se obtin astfel
5 cartonase.
|
Timp maxim de executie/test:
0.1 secunde
prof. Rodica
Pintea
Liceul "Grigore
Moisil" Bucuresti
Contact:ro_dica@yahoo.com
