spirala
Fie ABCD
un dreptunghi de coordonate A(0; 0), B(0; 1), C(k; 1), D(k;
0). Sa numim acest dreptunghi "dreptunghi de indice 1". Proportia
dintre lungimile laturilor sale este 1 : k.
Un al doilea dreptunghi ("dreptunghi de indice 2 ") este construit
pe latura de "Nord" a primului dreptunghi (BC) respectând
aceeasi proportie între lungimile laturilor sale (1 : k). Acest
dreptunghi este BEFC.
|BC|: |BE| = 1 : k.
Acum, latura "Vest" a dreptunghiului AEFD este AE. Cel
de al treilea dreptunghi este construit pe aceasta latura, respectând
proportia initiala între lungimile laturilor (1 : k). Acest
dreptunghi va fi dreptunghiul AGHE.
|AE|:|AG| = 1 : k. |
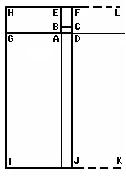 |
În mod asemanator
se construiesc noi dreptunghiuri pe laturile comune obtinute la pasul anterior,
respectând proportia initiala si secventa de directii în continuare
("Sud", "Est", "Nord", "Vest",
"Sud", ...).
Cerinta
Scrieti un program care, având ca date de intrare trei valori întregi
k, x,
y, determina indicele dreptunghiului
construit dupa metoda anterioara (proportia laturilor fiind 1 : k) care
contine punctul P(x, y).
Daca punctul P se afla pe una dintre laturile dreptunghiului se considera ca
el apartine dreptunghiului.
Date
de intrare
Fisierul de intrare spirala.in
contine o singura linie pe care se gasesc, în ordine, valorile intregi
k, x,
y separate prin câte un
spatiu.
Date de iesire
Fisierul de iesire spirala.out
contine o singura linie pe care se afla indicele dreptunghiului cerut.
Restrictii
1 <= k <= 100
-1 000 000 < x, y < 1 000 000
Exemple
| spirala.in |
spirala.out |
spirala.in |
spirala.out |
spirala.in |
spirala.out |
| 3 0 1 |
1 |
2 7 -2 |
5 |
4 1 17 |
2 |
Timp
maxim de executie/test: 0.1 secunde
Limite
de memorie: total memorie disponibila 15 Mb, din care pentru stiva maxim:
1 Mb
prof. Marinel
Serban
Liceul de Informatica "Gr. C. Moisil" Iasi
e-mail: marinel_serban@yahoo.com
